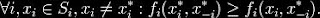>Let (S, f) be a game with n players, where S_i is the strategy set for player i, S=S₁ X S₂ … X S_n is the set of strategy profiles and f=(f₁(x), …, f_n(x)) is the payoff function for x S. Let x_ibe a strategy profile of player i and x_-i be a strategy profile of all players except for player i. When each player i {1, …, n} chooses strategy x_i resulting in strategy profile x = (x₁, …, x_n)then player i obtains payoff f_i(x). Note that the payoff depends on the strategy profile chosen, i.e., on the strategy chosen by player i as well as the strategies chosen by all the other players. A strategy profile x^* S is a Nash equilibrium (NE) if no unilateral deviation in strategy by any single player is profitable for that player, that is

A game can have either a pure-strategy or a mixed Nash Equilibrium, (in the latter a pure strategy is chosen stochastically with a fixed frequency). Nash proved that if we allow mixed strategies, then every game with a finite number of players in which each player can choose from finitely many pure strategies has at least one Nash equilibrium.

When the inequality above holds strictly (with > instead of ) for all players and all feasible alternative strategies, then the equilibrium is classified as a strict Nash equilibrium. If instead, for some player, there is exact equality between 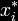and some other strategy in the set S, then the equilibrium is classified as a weak Nash equilibrium.